PoPL Lecture 7

In class

• We know the Well-foundedness Property of Inductive Terms: There is no inductive term T s.t. T is a proper subterm of itself:
  • So we can’t have terms like T = g(T)

  • But we might a term like that for streams

       g←┐    Circular terms
       └─┘
    

  • The following is seemingly an aside. Skip if you need to.

    • Consider the following definition

      TREE             DAG
        f               f
      ₁/ \₂            ( )
      a   a             a
      -----           -----
      f a a           f a a
      

      In the DAG, the ‘a’ is shared. It is like

      (define (a) (list 'a))
      (define (f t1 t2) (list 'f t1 t2))
      (let ([t (a)])
        (f t t))
      

      But in the tree form, it is more

      (let ([t1 (a)]  
            [t2 (a)])
        (f t1 t2))
      ;; note that t1 and t2 are different
      > (eq? (a) (a))
      #f
      > (equal? (a) (a))
      #t
      

      Term Graphs

And defining them in terms of equations

• Term Graphs: A term graph over a signature Σ is a structure <V, h, →> where
  1. V is a set of vertices
  2. h: V → Σ (head)
  3. → ⊆ V x N₁ x V (v,i,v’ written as v-i->v’)
  4. if h(v) ∈ Σ⁽ⁿ⁾, then v has exactly n out-edges. For each i: 1≤i≤n, there is exactly⁾, then v has exactly 1 out-edge labelled i.
• Defining some notation:
  • if h(v) = f and
  • f ∈ Σ⁽ⁿ⁾ and
  • v -i-> v_i for 1≤i≤n

  • Then, we write this as

    v ≅ f(v₁ … v_n) (≅ is actually ‘=’ with a dot on top)

• Consider examples:

        (f)t₁     v = {t₁ t₂ t₃} │ t₂ ≅ a()
       ₁/ \₂      h = { t₁ → f   │ t₃ ≅ b()
    t₂(a) (b)t₃         t₂ → a   │ t₁ ≅ f(t₂ t₃)
    G=<v,h,→>           t₃ → b } │ ─────────────
                                 │ this is a term
                                 │ graph written down
                                 │ as a set of equations
      
  f has arity 2, so it needs 2 out-edges
    
  We can also have
      (g)←┐
      └───┘
  

  For another example, we can see:

  

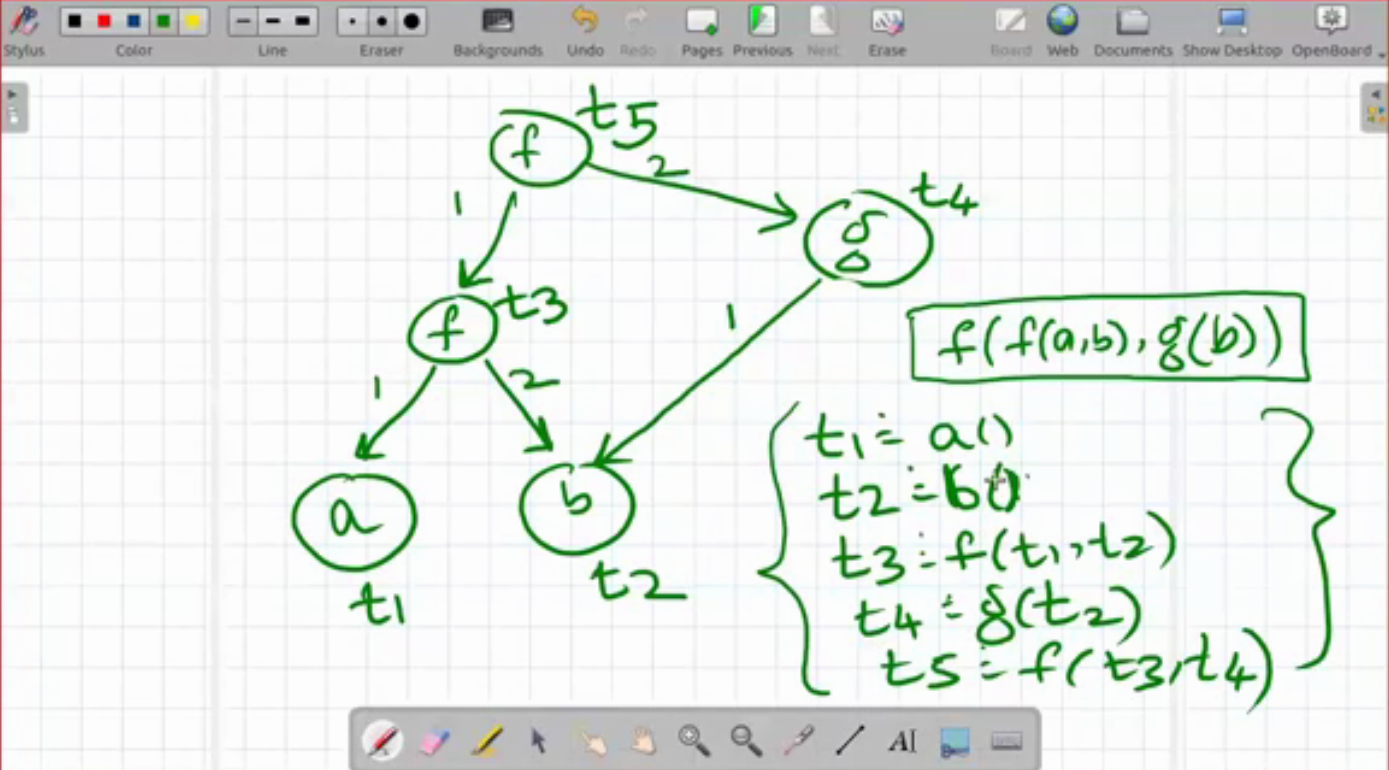
Path/Position

• From the term graph above, we can write something like t₅ ─²→ t₄ ─¹→ t₂
• A simpler way to do that is t₅ ─²¹→ t₂
• This ²¹ is called the path/position
• The path 21 takes t₅ to t₂

• REF rule:

  v ─[]-> v

  TRANS rule:

  v' ─[p]→ v'' and v ─[i]→ v', then

  v ─[i.p]→ v''

• Now, also:

  if v ─[p]→ r and v ─[p]→ s, then r == s

• TODO after this
• Position space
• paths == position
• pos(t1): all paths to all accessible vs.
• Term can be reconstructed from pos v and → ∑

• Position space: set of positions p, prefix closed: for all terms of the set, each prefix is also a term in the set. Motivation: Eliminating v

  Basically defines term v, without the v. 1 Position space defines a term graph’s subtree.

• Behaviour: mapping from terms to ∑, but upwards complete. Interaction.
• term over Σ is a behavious over Σ

Behaviour